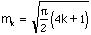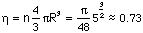Magic Numbers in Short-Range Order Structure.
S.L.Isakov
For all structure factors of amorphous systems we see common behaviour in first and second oscillations, namely splitted second peak at 1.7 and 2.0 in respect to the first maximum. What is the numbers? Obviously they have simple geometrical sense and no more. But let me look at the problem in another slice.
Note the remarkable similarity between the structure factor S(Q) for the ordinary amorphous system like Ni and its pair correlation function g(r) defined as:
 (1)
(1)
and reverse Furie-transform
 (2)
(2)
This similarity would not astonish us in the case of crystalline solids, for example, with simple hexagonal lattice. In this case g(r) coincides with S(Q) with x-scaling if (c/a)2= (├3)/2. In the case of amorphous solids we have no lattice, but we have approximating equality g(r/a)=S(Qa). Substitute it in (2) and compare with (1). These equations becomes equal if
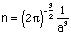 (3)
(3)
If we define
 where x=r/a or Qa
where x=r/a or Qa
then we have some equation
 (4)
(4)
which have many solutions, and some of them
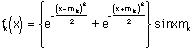 (5)
(5)
where
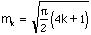
�
Atomic diameter equal to the first maximum, so it may be assigned to m1a/2. And then we can calculate atomic packing density
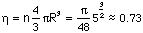
which is in very good agreement with the density of most amorphous alloys.
Calculate other value mk:
|
k
|
m(k)/m(1)
|
|
|
0
|
0,45
|
min
|
|
1
|
1
|
max
|
|
2
|
1,34
|
min
|
|
3
|
1,61
|
max
|
|
4
|
1,84
|
min
|
|
5
|
2,05
|
max
|
This magic number seems to be alike to those in real S(Q) and g(r). This arise from alike behaviour this function to those mentioned above.

ąĪą░ą╣čé čāą┐čĆą░ą▓ą╗čÅąĄčéčüčÅ čüąĖčüč鹥ą╝ąŠą╣
uCoz (1)
(1) (2)
(2)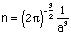 (3)
(3) where x=r/a or Qa
where x=r/a or Qa (4)
(4)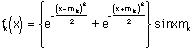 (5)
(5)